|
Approximations
for Liquids:
|
|
| Specific Volume |  |
| Specific Internal Energy |  |
| Specific Enthalpy |  |
As shown in the figure on the right, when the ratios  are
extrapolated to zero pressure, we have |
 |
||
|
|
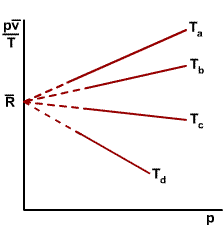Eqn.
(*)
|
||
|
where
|
 , |
||
 ,
and |
|||
| M = molecular weight | |||
Note: 
is
the universal gas constant, and it is the same for all gases.
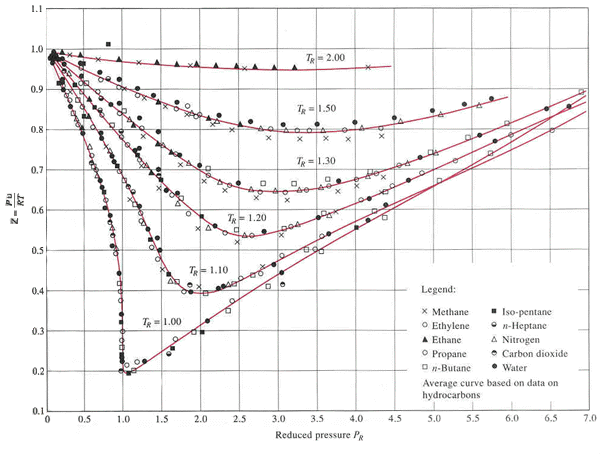
Compressibility
chart for various gases
Reference:
Cengel, Y. A. and Boles, M. A., "Thermodynamics: An Engineering Approach",
3rd ed., WCB/McGraw-Hill, Boston, 1998.
The compressibility factor
is defined as 
.
Eqn (*) can then be written in terms of the compressibility factor as
follows:
From the compressibility chart,
it can be observed that 
when the reduced pressure
and the reduced temperature 
.
[
and 
are the
critical pressure and
critical temperature, respectively.]
... and
B, C, D, ... are virial coefficients which account for the force interactions
among molecules. Z measures
the departure from the ideal gas equation of state.
When , the
force interactions between molecules are no longer significant.
|
Ideal
Gas
|
||
| - The gas consists of molecules that are in random motion and obey the laws of mechanics. | ||
| - The total number of molecules is large, but the volume of the molecules is a negligibly small fraction of the volume occupied by the gas. | ||
| - No appreciable forces act on the molecules except during the collisions. |
|
Equation
of State (Z=1)
|
|
| Equations in Different Forms: | pv = RT |
| pV = mRT | |
| PV = nRT | |
| Note: |
Equation of state requires the use of absolute temperature and absolute pressure. |
| For Ideal Gases: | u = u(T) |
| h = h(T) = u(T) + pv = u(T) + RT | |
|
Specific
Heat
|
Energy required to raise the temperature of a unit mass of a substance by one degree |
|
Specific
Heat at Constant Volume
|
 |
|
Specific
Heat at Constant Pressure
|
 |
|
Specific
Heat Ratio
|
 |
|
For
Ideal Gas:
|
|
|
Specific
Heat at Constant Volume
|
 
 |
|
Specific
Heat at Constant Pressure
|
 |
|
Relationship
Between Specific Heat at Constant Volume and Constant Pressure
|
From
the definition of the enthalpy, we have h = u + pv = u + RT
 |
|
Expressed
in Terms of Specific Heat Ratio
|
Since |
,
we have 
and
|
Ideal
Gas
|
||
|
Specific
Enthalpy
|
where Therefore, we have |
|
|
Polynomial
Form of Specific Heat at Constant Pressure as a Function of Temperature
|
|
|
|
Change
in Specific Internal Energy
|
 |
|
|
Change
in Specific Enthalpy
|
 |
|
|
Specific
Heat at Constant Volume
|
 |
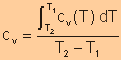OR
use the specific heat evaluated at the average temperature over the interval. |
|
Specific
Heat at Constant Pressure
|
 |
|
=0K
and 
=0
are the reference temperature and reference
value for specific enthalpy, respectively.
(300 K < T < 1000 K)
are given in the following table.
 |
|||||
|
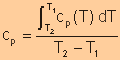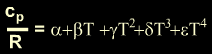where
T is in Kelvin and the above equation is valid where 300
K < T < 1000 K
|
|||||
|
Gas
|
 |
 |
 |
 |
 |
|
CO
|
3.710
|
-1.619
|
3.692
|
-2.032
|
0.240
|
 |
2.401
|
8.735
|
-6.607
|
2.002
|
0
|
 |
3.057
|
2.677
|
-5.810
|
5.521
|
-1.812
|
 |
4.070
|
-1.108
|
4.152
|
-2.964
|
0.807
|
 |
3.626
|
-1.878
|
7.055
|
-6.764
|
2.156
|
 |
3.675
|
-1.208
|
2.324
|
-0.632
|
-0.226
|
|
Air
|
3.653
|
-1.337
|
3.294
|
-1.913
|
0.2763
|
 |
3.267
|
5.324
|
0.684
|
-5.281
|
2.559
|
 |
3.826
|
-3.979
|
24.558
|
-22.733
|
6.963
|
 |
1.410
|
19.057
|
-24.501
|
16.391
|
-4.135
|
 |
1.426
|
11.383
|
7.989
|
-16.254
|
6.749
|
|
Monatomic
Gases
|
2.5
|
0
|
0
|
0
|
0
|
Reference: Moran, M. J. and Shapiro, H. N., "Fundamental of Engineering Thermodynamics," 2nd ed., John Wiley & Sons, Inc., New York, 1992. pp.718 |
|||||
|
Polytropic
Process
|
|
|
Equation
Form
|
 =constant |
|
Work
Done (
 ) |
 |
|
Work
Done (n=1)
|
 |
|
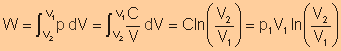Polytropic
Process of an Ideal Gas
|
|
|
Work
Done (
) |
 |
|
Work
Done (n=1)
|
 |
|
Relationship
of T with p and V
|
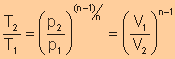(Derivations are shown in the next table) |
|
Derivations
|
|
|
Relationship
Between T and V
|
Relationship
Between T and p
|
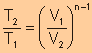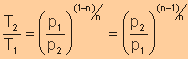=constant =constant =constant =constant |
=constant =constant =constant  |