Any device that violates either the first or the second law of thermodynamics
is called a perpetual-motion machine.
Despite numerous attempts, no perpetual-motion machine is known to have worked. But this has not stopped inventors from trying to create new ones.
A device that violates the first law of thermodynamics (by creating energy)
is called a perpetual-motion machine of the first kind.
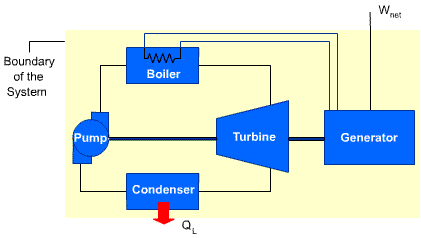
A device that violates the second law of thermodynamics is called a perpetual-motion
machine of the second kind.

A process which can be reversed without leaving any trace on the surroundings.
That is, both the system and the surroundings are returned to their initial
states at the end of the reverse process. This is possible only if the
net heat and net work exchange between the system and the surroundings
is zero for the combined process (original and reverse).
A system can be restored to its initial state following a process, regardless of whether the process is reversible or irreversible. But for reversible process, their restoration is made without leaving any net change on the surroundings.
Reversible processes actually do not occur in nature. They are merely idealizations of actual processes.
When reversible processes are
used,
work-producing devices - deliver the most work
work-consuming devices - require the least work
The factors that cause a process to be irreversible are called irreversibilities.
|
Irreversibilities
|
||
| Friction | Mixing of two gases | Unrestrained expansion |
| Inelastic deformation of solids | Electric resistance | |
| Heat transfer across a finite temperature difference | Chemical reactions | |
For an adiabatic expansion/compression of a gas, the non- uniformity of
pressure will render this process non-quasi-equilibrium.
If the piston is pushed in very rapidly, the gas molecules near the piston face will not have sufficient time to escape, and they will pile up in front of the piston. This will raise the pressure near the piston face. Because of this higher pressure value at the piston face, a non-quasi-equilibrium compression process will require a larger work input than the corresponding quasi-equilibrium one.
When the process is reversed by letting the gas expand rapidly, the gas molecules in the cylinder will not be able to follow the piston as fast, thus creating a low-pressure region before the piston face. Because of this low-pressure value at the piston face, a non-quasi-equilibrium process will deliver less work than a corresponding reversible one.
Consequently, the work done by the gas during expansion is less than the work done by the surroundings on the gas during compression, and thus the surroundings have a net work deficit. When the piston returns to its initial position, the gas will have excess internal energy, equal in magnitude to the work deficit of the surroundings.
The system can easily be returned to its initial state by transferring this excess internal energy to the surroundings as heat. But the only way the surroundings can be returned to its initial condition is by completely converting this heat to work, which can only be done by a heat engine that has an efficiency of 100 percent. This, however, is impossible to do, since it would violate the second law of thermodynamics.
Since only the system, not both the system and the surroundings, can be returned to its initial state, we conclude that the adiabatic non-equilibrium expansion/compression of a gas is irreversible.
Consider a can of cold soda left in a warm room. Heat will flow from the
warmer room air to the cooler soda. The only way this process can be reversed
and the soda restored to its original temperature is to provide refrigeration,
which requires some work input. At the end of the reverse process, the
soda will be restored to its initial state, but the surroundings will
not be.
The internal energy of the surroundings will increase by an amount equal in magnitude to the work supplied to the refrigerator. The restoration of the surroundings to its initial state can be done only by converting this excess internal energy completely to work, which is impossible to do without violating the second law.
Since only the system, not both the system and the surroundings, can be returned to its initial state, we conclude that heat transfer through a finite temperature difference is an irreversible process.
It is physically impossible to have a reversible heat transfer process. But a heat transfer process becomes less and less irreversible as the temperature difference between the two bodies approaches zero.
A reversible heat transfer is a conceptual process and cannot be duplicated in the laboratory.
The smaller the temperature difference between two bodies, the smaller the heat transfer rate will be. Any significant heat transfer will require a very large surface and a very long time. Therefore, even though approaching reversible heat transfer is desirable from a thermodynamic point of view, it is impractical and not economically feasible.
The most efficient cycle are reversible cycles, i.e., cycles that consist
entirely of reversible processes.
Reversible cycles cannot be achieved in practice because irreversibilities associated with each process cannot be eliminated. However, reversible cycles provide upper limits on the performance of real cycles.
- the best known reversible cycle
- proposed in 1824 by French engineer Sadi Carnot
- is composed of four reversible processes, two isothermal and two adiabatic.
|
Process
1-2
|
Reversible isothermal expansion | |
|
Process
2-3
|
Reversible adiabatic expansion | |
|
Process
3-4
|
Reversible isothermal compression | |
|
Process
4-1
|
Reversible adiabatic compression | |
The Reversed Carnot Cycle - Carnot Refrigeration Cycle
|
Carnot
Principles
|
||
| 1. The efficiency of an irreversible heat engine is always less than that of a reversible one operating between the same two reservoirs. | ||
| 2. The efficiencies of all reversible heat engines operating between the same two reservoirs are the same. |
The violation of either statement results in the violation of the second law of thermodynamics.
 |
 |