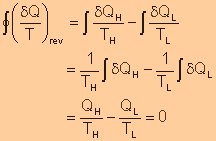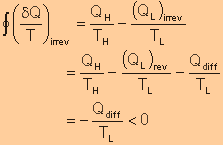| First Law of Thermodynamics |
Energy
|
|
| Second Law of Thermodynamics |
Entropy
|
|
Unlike energy, entropy is a nonconserved property. |
||
|
Clausius
Inequality
|
|
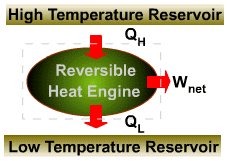
| The cyclic
integral of |
|
| This inequality is valid for all cycles, reversible or irreversible. | |
| The symbol
|
|
| Any heat flow
to or from a system can be considered to consist of differential amounts
of heat. The cyclic integral of |
|
|
 |
||||
|
 |
||||
![]()
If a quantity whose cyclic integral is zero depends on the state only and not the process path, then it is a property.
![]()
![]()
A, B are any two internally reversible process paths between states 1 and 2.
![]() (S: Entropy)
(S: Entropy)
S is an extensive property of a system. Entropy per unit mass, designated s, is an intensive property.
![]()
To perform the integration, one needs to know the relation between Q and T during a process.
The integral of ![]() will
give us the value of entropy change only if the integration is carried
out along an internally reversible path between two states.
will
give us the value of entropy change only if the integration is carried
out along an internally reversible path between two states.
The integral of ![]() along
an irreversible path is not a property, and in general, different values
will be obtained when the integration is carried out along different irreversible
paths.
along
an irreversible path is not a property, and in general, different values
will be obtained when the integration is carried out along different irreversible
paths.
![]()
![]() is
the value of entropy specified at the reference state.
is
the value of entropy specified at the reference state.
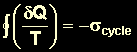 (
( |
||
|
Reversible
Cycles
|
|
|
|
Irreversible
Cycles
|
|
|
|
Impossible
Cycles
|
|
|
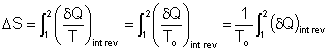
![]()
The entropy change of a system during an internally reversible process can be positive or negative depending on the direction of heat transfer. Heat transfer to a system (Q > 0) will increase the entropy of that system whereas heat transfer from a system (Q < 0) will decrease it. In fact, losing heat is the only way the entropy of a system can be decreased.
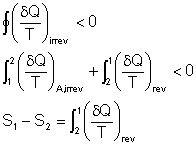
![]()
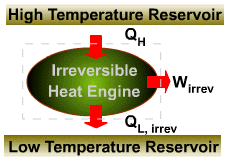
The entropy change of a closed
system during an irreversible process is greater than the integral of
![]() evaluated
for that process.
evaluated
for that process.
![]()
For an adiabatic process, Q = 0
![]()
The entropy of an adiabatic closed system always increases or, in the limiting case, remains constant during a process.
In the absence of any heat transfer, entropy change is due to irreversibilities only, and their effect is always to increase the entropy.
A General Case
A system plus its surroundings constitutes an adiabatic system, assuming both can be enclosed by a sufficient large arbitrary boundary across which there is no heat or mass transfer.
![]()
which is applicable to both closed or open (control volume) systems.
The total entropy change associated with a process must be positive or zero. The equality holds for reversible processes and the inequality for irreversible processes.
The above equation does not imply that the entropy of a system or the surroundings cannot decrease. It only implies that their sum cannot decrease.
|
|
||
|
Reversible
Processes
|
= 0
|
|
|
Irreversible
Processes
|
> 0
|
|
|
Impossible
Processes
|
< 0
|
|
The more irreversible a process is, the larger the entropy is generated
during the process
|
Causes
of Entropy Change
|
|
|
Heat
Transfer
|
|
|
Irreversibilities
|
|
Isentropic
Process
|
|
|
If a process
involves no heat transfer (adiabatic) and no irreversibilities within
the system (internally reversible), the entropy of a system must
remain constant during that process. Such a process is called an
isentropic process.
|
|
|
Remarks
about Entropy
|
|
| 1. Process
can occur in a certain direction only, not in any direction. A process
must proceed in the direction that complies with the increase-in-entropy
principle, that is, |
|
| 2. Entropy is a nonconserved property, and there is no such thing as the conservation of entropy principle. Entropy is conserved during the idealized reversible processes only and increases during all actual processes. | |
| 3. The performance of engineering system is degraded by the presence of irreversibilities, and the entropy generation is a measure of the magnitude of the irreversibilities present during that process. |
Entropy can be viewed as a measure of molecular disorder, or molecular
randomness.
Heat is, in essence, a form of disorganized energy, and some disorganization (entropy) will flow with heat.
Work instead is an organized form of energy, and is free of disorder or randomness and thus free of entropy. There is no entropy transfer associated with energy transfer as work.
The quantity of energy is always preserved during an actual process (the first law), but the quality is bound to decrease (the second law). This decrease in quality is always accompanied by an increase in entropy.
From a statistical point of view, entropy is a measure of molecular randomness, i.e., the uncertainty about the position of molecules at any instant. Even in the solid phase, the molecules of a substance continually oscillate, creating an uncertainty about their position.
|
Third
Law of Thermodynamics
|
| The entropy of a pure crystalline substance at absolute zero temperature is zero since there is no uncertainty about the state of the molecules at that instant. |
The third law of thermodynamics provides an absolute reference point for the determination of entropy.