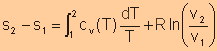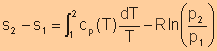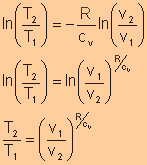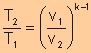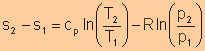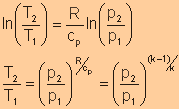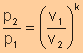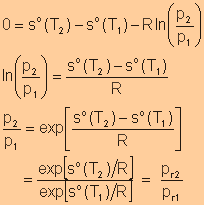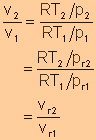LECTURE 14
14.1 Tabular Entropy Data


 
Two-Phase
Liquid-Vapor Mixture
 
Compressed Liquid

Reference State:

For water: triple point (0.01 )
For refrigerants: -40 (-40 )

 
14.2 Graphical Entropy Data
14.2.1 Temperature-Entropy Diagram


Energy transfer by heat can be represented as an area on a T-S diagram.

 
14.2.2 Enthalpy-Entropy Diagram (Mollier Diagram)


Mollier diagram is intended for evaluating properties at superheated vapor states and for two-phase liquid-vapor mixture.

 

 
14.3 Two Important Thermodynamic Relations


 
First Law of Thermodynamics
Definition of Enthalpy

 
14.4 Entropy Change of an Ideal Gas


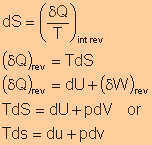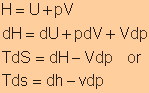Two Different Expressions for Entropy Change of an Ideal Gas

For an ideal gas, we have

and . The first equation can then be written as

For an ideal gas, we have

and . The first equation can then be written as


Definition
Standard-State Entropy

 

 
Entropy Change of an Ideal Gas in Terms of the Standard-State Entropy


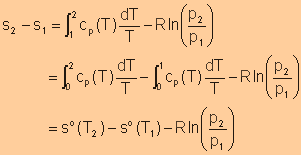Note: Reference State: 1 atm and 0K

 

 
Table A-17
pp. 923-924
 Ideal Gas Properties of Air
Table A-18
to
Table A-25
pp. 925-936
 Ideal Gas Properties of Other Gases

 

 
14.5 Carnot Cycle in T-s Diagram

 
14.6 Isentropic Processes of Ideal Gases


Isentropic Processes of Ideal Gases with Constant Specific Heats

Expression a

Expression b

For isentropic processes, the change of entropy is zero, thus we have

For an ideal gas,
and , which yield .

Finally, we have

For isentropic processes, the change of entropy is zero, thus we have

 
Expression c

Equate expression a and expression b, we have

constant

 
Polytropic Process
n = 0
Isobaric Process (Constant-Pressure)
n = 1
Isothermal Process (Constant-Temperature)
n = k
Isentropic Process (Constant-Entropy)
n =
Isometric Process (Constant-Volume)

 
Isentropic Processes of Ideal Gases with Variable Specific Heats
Relative Pressure
Relative Volume


where is a function of temperature, and is the relative pressure.

Note: is not truly a pressure, the name "relative pressure" is somewhat misleading. Do not confuse with the reduced pressure of the compressibility diagram.


where is also a function of temperature , and is the relative volume.

Note: Do not confuse with the pseudoreduced specific volume of the compressibility diagram.