The term "availability" was made popular in the United States by MIT School
of Engineering in the 1940s.
An equivalent word "exergy" was introduced in Europe in the 1950s.
Availability - work potential, maximum useful work
Work = f(Initial state, Process path, Final state)
In the availability analysis, the initial state is specified.
To maximize the work output:
- the process to be executed is reversible
- the final state is a dead state
If the state of a system departs from that of the environment, an opportunity exists for developing work. However, as the system changes state toward that of the environment, the opportunity diminishes, ceasing to zero when the two are in equilibrium with one another.
A system is said to be in the dead state when it is in thermodynamic equilibrium with its surroundings.
| At the dead state: |
| 1. A system is at the same temperature and pressure of its surroundings (in thermal and mechanical equilibrium); |
| 2. It has no kinetic or potential energy relative to its surroundings (zero velocity and zero elevation above a reference level); |
| 3. It does not react with the surroundings (chemically inert); |
| 4. There are no unbalanced magnetic, electrical and surface tension effects between the system and its surroundings (mechanical equilibrium). |
A system has zero availability at the dead state.
The properties of a system
at the dead state are denoted by subscript zero, for example, ![]()
Dead state temperature![]()
Dead state pressure![]()
We can conclude that:
A system will deliver the maximum possible work as it undergoes a reversible
process from the specified initial state to the state of its environment,
i.e., the dead state.
Availability does not represent the amount of work that a work- producing device will actually deliver upon installation. Rather, it represents the upper limit on the amount of work a device can deliver without violating any thermodynamic laws.
There will always be a difference between availability and the actual work delivered by a device. This difference represents the room engineers have for improvement.
The availability of a system at a specified state depends on the conditions of the environment (the dead state) as well as the properties of the system. Therefore, availability is a property of the combined system, the system and its surroundings, and not of the system alone.
Altering the environment is another way of increasing availability, but it is definitely not an easy alternative.
When a system is expanding and doing work, part of the work done is used
to overcome the atmospheric pressure,
![]()
![]() in
this case, represent a loss. Therefore, the work done by the system is
not entirely in a useful form,
in
this case, represent a loss. Therefore, the work done by the system is
not entirely in a useful form,
Useful work![]()
However, when a system is compressed, the atmospheric pressure helps the compression process, and thus Wsurr represents a gain.
Note that the work done by or against the atmospheric pressure has significance only for systems whose volume changes during the process.
Reversible work is defined as the maximum amount of useful work can be obtained as a system undergoes a process between the specific initial and final states.
This is the useful work (output or input) obtained when the process between the initial and final states is executed in a totally reversible manner.
Any difference between the
reversible work ![]() and the the useful work
and the the useful work ![]() is due to the irreversibilities present during the process, and this difference
is called irreversibility.
is due to the irreversibilities present during the process, and this difference
is called irreversibility.
Irreversibility![]()
Irreversibility can be viewed as the lost opportunity to do work. It represents the energy that could have been converted to work but was not. The smaller the irreversibility associated with a process, the greater the work that will be produced.
For a totally reversible process, the actual and reversible work are identical, and thus irreversibility is zero.
For all actual processes, irreversibility is a positive quantity.
First Law
![]()
Second Law
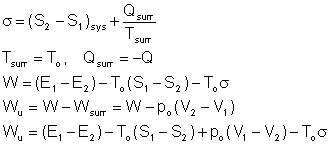
If the process is executed in a reversible manner between the same initial and final states, and in the same environment,
![]()
The useful work done during this process is the reversible work Wrev
![]()
This is the maximum useful work that can be done as the system changes from state 1 to state 2.
If the state 2 is the dead state
 (Availability)
(Availability)
The availability of a closed
system at the dead state![]() is zero. That is, no work can be extracted from a system which is in equilibrium
with its surroundings. Note that these relations are applicable to nonreacting
systems.
is zero. That is, no work can be extracted from a system which is in equilibrium
with its surroundings. Note that these relations are applicable to nonreacting
systems.
![]()