| |
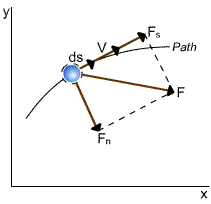 |
|
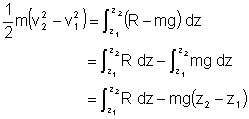 |
 |
|
If R=0
![]()
![]()
the sum of the kinetic and gravitational potential energy remains constant.
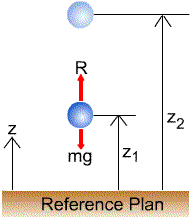
![]()
Thermodynamic definition of work:
Work is done by a system on its surroundings if the sole effect on everything external to the system could have been the raising of a weight.
the raising of a weight = a force acting through a distance
the test of whether a work interaction has taken place is not that the elevation of a weight has actually taken place, or that a force has actually acted through a distance, but that the sole effect could have been an increase in the elevation of a weight.
Work is a means of transferring energy.
Sign Convention:
|
W > 0, if work is done by the system W < 0, if work is done on the system |
||
Process Path : the series of equilibrium states through which a system passes during a process.
To describe a process completely, one should specify the initial and final states of the process, as well as the path it follows, and the interactions with the surroundings.
To evaluate the integral, it is necessary to know how the force varies with the displacement. The value of W depends on the details of the interactions taking place between the system and surroundings during a process and not just the initial and final states of the system.
Work is not a property of the system or the surroundings.
The notion of work at a state has no meaning.
![]()
The differential of work is inexact since the integral can not be evaluated without specifying the details of the process.
![]()
The differential of every property is exact.
The rate of energy transfer by work is called power.
![]()
![]()
For a piston-cylinder assembly
![]()
Expansion: dV>0, ![]()
Compression: dV<0,![]()
![]()
It is applicable to systems of any shape provided the pressure is uniform over the moving boundary.
To perform the integration, it requires a relationship between the pressure and volume.
Example: ![]() constant
(polytropic process)
constant
(polytropic process)
n = 0 :constant pressure
n = 1 :constant temperature
A system is called a simple compressible system in the absence of electrical,
magnetic, gravitational, motion and surface tension effects.
At an equilibrium state, the
values of the intensive properties are uniform throughout the system.
State Postulate : number of properties required to fix the state of a
system.
The state of a simple compressible system is completely specified by two independent, intensive properties.
temperature & specific volume - two independent properties
temperature & pressure - two
independent properties for single- phase systems, but not for two-phase
systems.
|
Initial state: Final state: The work done is given
by |
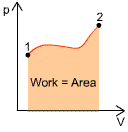 |
|