Small-Angle X-Ray Scattering

Around the turn of the 20th century, Röntgen discovered radiation with wavelength much smaller than that of visible light. Röntgen named this high-energy radiation “x-rays” because of their unknown nature. Soon after this discovery, von Laue and his associates discovered that crystals scatter x-rays in distinct patterns. It was quickly recognized that these patterns give direct insight into the structure of the materials that caused the scattering. Since these early discoveries, many technical advances made x-ray scattering one of the most powerful characterization tools available for both homogeneous and heterogeneous materials. Today, scattering from x-rays, neutrons and light is used by scientists in many different disciplines to study a vast range of materials ranging from polymers to proteins.

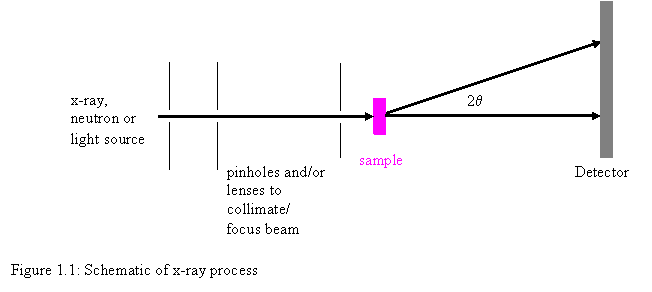
Small-Angle Scattering (SAS) experiments generally follow this procedure as shown in Figure 1.1: irradiate a sample with a well-collimated beam of some type of radiation (x-rays, neutrons or light), measure the resulting intensity as a function of angle between the incoming beam and scattered beam, then determine the structure that caused the observed pattern. Scattering patterns are caused by the interference of secondary waves that are emitted from various structures (electrons for x-rays and light, or nuclei for neutrons) when irradiated. Scattering of x-rays is caused by differences in electron density, scattering of neutrons is caused by differences in scattering power of different nuclei and scattering of light is caused by differences in refractive index. Since the larger the diffraction angle the smaller the length scale probed, wide angle x-ray scattering (WAXS) is used to determine crystal structure on the atomic length scale while small-angle x-ray scattering (SAXS) or small-angle neutron scattering (SANS) is used to explore microstructure on the colloidal length scale. Light is used similarly but because the wavelength of light is much greater than that of x-rays or neutrons, light scattering is used for much larger structures like the phases in blends of elastomers or particle size distributions.

Unlike an electron micrograph, small-angle x-ray scattering patterns do not give morphological information directly. The result of a SAXS experiment is essentially the intensity of the Fourier transform of the electron density and must be interpreted in order to determine morphology. One fundamental problem with any scattering experiment is that two different morphologies can, in theory, give identical scattering patterns. Generally, one cannot reconstruct the exact microstructure uniquely from a SAXS pattern because in a scattering experiment only the scattered radiation intensity can be measured and all phase information is lost. Therefore, one cannot be absolutely sure that a scattering pattern is due to a particular morphology. Still however, usually something is known about the system in question, so that it is often (but not always!) reasonable to assume that if a particular model is shown to fit the scattering pattern, then the model is a correct description of the morphology. Nevertheless, many different approaches exist to extract morphological information from a SAXS pattern.

General Scattering Theory
When x-rays of known wavelength are scattered, a scattering vector, q, can be defined that is equal to 2p/l(S-So). This important definition is based on the wavelength of radiation, l, and unit vectors in the incident and scattered x-ray directions, respectively, So and S. As shown in Figure 1.1, the angle between So and S is 2q. Thus the resulting magnitude of the scattering vector, q, is equal to 4psinq/l. The scattering vector is the basis for all scattering equations.

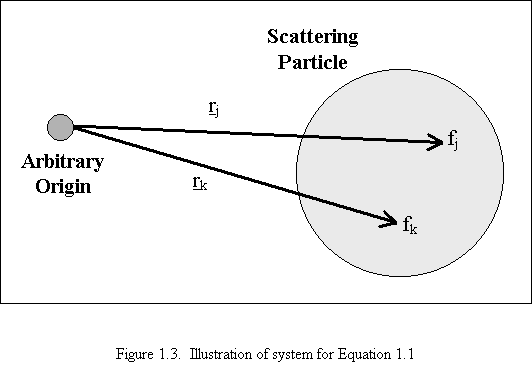
Incoherent or Compton scattering, which is virtually nonexistent at small angles, refers to scattered waves that have changed phase and wavelength. Neglecting Compton scattering (no phase change and no wavelength change), the coherent scattering of x-rays I(q) by a single fixed particle is mathematically represented by Equation 1.1 which is the fundamental scattering equation. In Equation 1.1, Ie(q) is the scattered intensity of a single electron measured in identical conditions as I(q). As shown in Figure 1.3, f_j and f_k are the scattering powers of the jth and kth atoms respectively. Also in Figure 1.3, r_j and r_k are vectors from some arbitrarily chosen origin to the center of the jth and kth atoms respectively.

The square root of the right hand side of Equation 1.1 is known as the form factor, F_k. Form factors have been derived analytically for many simple geometries. For example, the form factor for a sphere of radius R_s, is given in Equation 1.2. This expression was derived by Lord Rayleigh and is often denoted as F(qR) when used in complex scattering expressions. Some of the form factors with analytical expressions include cylinders (circular and oval cross sections), spheroids (prolate and oblate), spherical shells, concentric spherical shells, parallelepipedons, infinitely thin rods and infinitely flat circular disks.

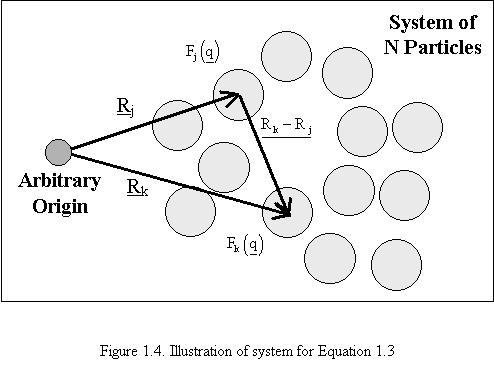
As particle density increases (particle volume divided by total volume), inter-particle interference becomes a factor, i.e. the scattering pattern depends on the locations of the individual particles. At high particle densities inter-particle interference can dominate the scattering curve. The Debye Equation describes scattering from multiple particle systems with inter-particle interference included. The Debye Equation is analogous to Equation 1.1 and is given in Equation 1.3. Equation 1.3 is based on the form factors of N different particles and a vector from the centers of the jth and kth scattering particles R_k-R_j as shown in Figure 1.4.

Equation 1.1 is based on scattering “points” and Equation 1.3 is based on scattering particles. Scattering “points” have no finite volume while scattering particles do have finite volume. Therefore when simulating scattering by choosing points, scattering “points” can be chosen randomly while the centers of scattering particles cannot, since the latter is limited by the fact that no two particles can occupy the same space.

Occasionally, it is desired determine scattering from a collection of anisotropic particles whose orientation is random. An example of this would be a dilute, quiescent solution of particles. Equations 1.4 and 1.5 result from Equations 1.1 and 1.3 respectively, after orientation averaging. In these equations q is the magnitude of the scattering vector, q. r_jk is the magnitude of the “point” to “point” vector, r_j-r_k, and R_jk is the magnitude of the particle center to particle center vector, R_j-R_k

Analysis of Scattering Data and Goals of this Research
Generally, analyzing an entire scattering pattern requires significant effort, and a number of different methods are used to analyze data. The purpose here is not to familiarize the reader with all these methods but rather to describe the most commonly used approaches. The reader should note that our Monte-Carlo methods can be used to calculate entire scattering patterns, and Monte-Carlo methods are applicable to almost any type of system; however these methods are very time consuming and hence should only be used when alternatives do not exist.

Morphologies without Interparticle Interference
Structural parameters from simple single-particle spherical morphologies can be determined in a matter of seconds using a least squares fit of Equation 1.2. In other words, a scattering curve is calculated from Equation 1.2, then it is smeared and compared to the experimental scattering pattern. This process is repeated until the calculated scattering curve most closely matches the experimental one, i.e. the sum of the squares of the differences between the experimental scattering points and the calculated scattering points is minimized. Essentially all real examples of identical single particles with perfect alignment are objects that also have analytical solutions, i.e. cylinders or spheroids, and can be solved with essentially the same procedure.

The first step in this research was to simulate scattering from these simple systems to prove that a Monte-Carlo method can in fact be used to simulate scattering. The most important outcome of this part of the research was in learning how to properly perform these simulations. The existence of analytical solutions allowed me to pinpoint errors in the code, allowed for the determination of simulation times required, and also aided in the choice of a random number generator. The paper published in the Journal of Applied Crystallography referenced below describes this effort.

If single particles are allowed to have a distribution of sizes or orientations, then the situation becomes quite complicated. Analytical methods can be used if spheres have a distribution of sizes and such methods have been applied to systems of Al-Li precipitates. Anisotropic objects with random orientation fall into two categories. Scattering patterns from some objects with random orientation have analytical solutions. Cylinders for example have been used to model dilute solutions of hemoglobin. Some objects with random orientation do not have analytical descriptions of the scattering pattern; these systems require Monte-Carlo simulations developed elsewhere. If the orientation of anisotropic objects is non-random, i.e. a fibrinogen system under shear, then there are no other approaches other than the Monte-Carlo approach e to describe the complete scattering pattern.

The ultimate goal of this research is to develop a Monte-Carlo method that is able to fit real experimental data using the approach given in this thesis. For the simplest systems, i.e. identical single particles that are infinitely symmetric (spheres) or identical single particles with perfect alignment, this goal could currently be reached if a suitable least-squares routine were developed. The former could probably be coded and run on a fast PC, while the latter is obviously more time-consuming because an entire two-dimensional pattern is necessary. On a PC, many weeks would be required to fit a two-dimensional scattering pattern with a Monte-Carlo model, which is too far long to be of practical use. However a high-speed supercomputer could perform this function in a reasonable amount of time. Practically, there is no reason to develop such a routine for these systems because simpler methods exist to analyze scattering data from these systems.

For both multiple-electron density systems and anisotropic objects with preferred orientation, there would be definite practical benefit in developing least-square routines to fit real experimental data. Systems such as elongated micelles, and voids in elongated polymers presumably would scatter without interparticle interference, and currently there are no good methods to analyze data from such systems. However, the many weeks of simulation time for a perfectly oriented system could possibly increase by an order of magnitude for a system with non-perfect orientation.

Morphologies with Interparticle Interference
Dense multiple particle systems are most commonly found in solid polymers and have two-dimensional SAXS patterns like that shown in Figure 1.5. Analysis of scattering from dense multiple particle systems is extremely difficult. Normally, if the dense multiple scattering systems are comprised of spheres then the analytical expression derived by Zernicke and Prins. Because no other approaches exist, scattering from systems of dense anisotropic scattering particles has to be analyzed using a Monte-Carlo method. Monte-Carlo data analysis for systems of dense anisotropic scattering particles is done using Equation 1.3 or Equation 1.5. One problem in simulating scattering from dense anisotropic systems is that Equation 1.3 is valid for only a single arrangement of particles and thus, a large number of particles are required in the simulation. Equation 1.3 is also a function of a double summation over all scattering particles. Comparing small systems of 100 particles and 1000 particles, the 1000 particle systems would take 100 times longer to calculate using Equation 1.3. To generate the entire scattering pattern from a single arrangement of particles would take nearly a year for system with tens of millions of particles, which I think is the size required for accurate statistics. Another problem is that it can be very difficult to get high particle densities by merely placing particles. In our lab it has taken several days to get particle densities near 0.4 for approximately 1 million spheres by random placement. These demands make computer simulation of scattering from these kinds of systems impossible.

To give the reader a better understanding why a Monte-Carlo methods might be a good tool to analyze scattering data , the general ideas of Monte-Carlo techniques need to be explored. This section should help the reader understand why a Monte-Carlo technique is a much more time-consuming approach to SAXS data analysis.

A Brief Description of the Monte-Carlo Method
Generally, a Monte-Carlo method is a technique to solve a complex problem by the observation of a random process whose parameters are based on the complex problem. Monte-Carlo methods are therefore based on the sampling of the devised random process. The following description should clarify this definition. Consider the task of choosing points in space to simulate a sphere with a radius equal to 10 cm. The points in space, once chosen, will then be used as scattering points. One quickly realizes that a real sphere is a continuous object while a sphere simulated via “points in space” is nothing more than a concentration of discrete points. At first thought, it may seem easiest to accomplish this goal by either building a sphere from spherical shells or from a grid of points, however, a Monte-Carlo method can also be employed. Figure 1.6 is a visualization of these three ideas.

To build a sphere from spherical shells the following must be done.
    1. Select an origin.
    2. Build a very small shell around this origin with points in space.
    3. Continue to build larger shells that are equidistant and concentric about the origin until the radius of 10 cm is met.
To use a grid approach the following must be done.
    1. Arrange a grid of points larger than 20 cm x 20 cm x 20 cm and choose the center of the grid as the origin.
    2. Choose every point whose distance from the origin less than or equal to 10 cm.
    3. Use the chosen points in space as scattering points.
Using a Monte-Carlo method, this problem would be approached in the following manner.
    1. For some box larger than 20 cm x 20 cm x 20 cm, choose the center as the origin.
    2. Randomly select points inside (or on the surface) the box.
    3. If the distance between the origin and random point is less than or equal to 10 cm then use the random point as a scattering point.

There are problems with the “shell” and “grid” methods that the Monte-Carlo method overcomes. In the “shell” method the problem is that the distance between the discrete shells causes artifacts in the scattering pattern. Also, it is very difficult to get a constant point density with this method. In other words, as the shells get smaller the number of points that are needed per shell is a function of the cube root of the radius, hence how does one maintain that the number of points is a whole number. In the “grid” method, artifacts caused by the regular grid can be seen in the scattering. Also, the exterior of the sphere is very rough because the sphere is made from a cubic grid of points, this gives poor scattering results because the scattering curve is very sensitive to what happens at the edge. Therefore, the act of choosing random points to simulate the sphere is by far the most appropriate choice.

However, true randomness is impossible to achieve with random number generators normally available on computers. To best illustrate the non-random behavior, one could use a spreadsheet program to draw four random numbers between zero and 100. The expected average of the four numbers should be approximately 50 with an approximately even distribution. If the first number drawn is roughly 20, the second number drawn is roughly 80 and the third number drawn is roughly 60, the spreadsheet will force the fourth number to be approximately 40. In other words, the (not so random) random number generator approximately forces the correct average and expected distribution. In other words the better the randomness of the number generator the longer the computer run time.

B.C. McAlister and B.P. Grady, "Simulation of Small Angle X-ray Scattering from Single Particle Systems", Journal of Applied Crystallography, 31, 594 (1998)

B.C. McAlister, B.P. Grady, “The Use of Monte-Carlo Simulations to Calculate Small-Angle Scattering Patterns”, Macromolecular Symposia, 190, 117 (2003).